Applied general equilibrium models
In their single-country form, applied general equilibrium (AGE) models simulate the variety of markets that compose entire economies. In their regional or global forms, these models also simulate the market transactions among economies or groups of economies. In all these cases, AGE models account for the interactions in markets for goods, services, labor, physical capital, and other productive inputs. A large and growing body of evidence suggests that the indirect and economywide effects of policy changes captured in this framework are indeed important, and there is a well-established theoretical foundation for the approach. Economywide effects include upstream and downstream production linkages through input-output relationships; intersectoral competition for basic resources such as labor, physical capital, and land; reallocation of rents from quantitative restrictions; distributional effects across household types; and exchange rate changes. AGE models provide a means of explicitly accounting for these effects in a comprehensive and consistent manner.
The Notion of ‘‘Applied’’
What is meant by the notion of ‘‘applied’’ in applied general equilibrium models? Francois and Reinert (1997) give the following four-part characterization:
Detailed policy orientation. Applied models use a broader set of policies than just ad valorem tariffs. Themodels involve an analytical commitment to the sectoral and institutionaldetails of a policy, including the role of data nomenclatures and concordances among nomenclatures, as well as a commitment to the policymaking process itself and sensitivity to the kinds of results that are of interest to policymakers.
Nonlocal changes form distorted base equilibria. In most theoretical analyses of trade and other economic policies, the economy begins in a nondistorted state with no tariffs, quotas, or other taxes present. To this initial nondistorted equilibrium an infinitesimal tariff or tax is introduced, and a new, counterfactual equilibrium is solved for using the linear approximation of differential calculus. In applied policy models, by contrast, the initial or base equilibrium reflects the relevant set of policy distortions. Since the policy changes introduced into the model are those actually under consideration rather thaninfinitesimal, the resultant changes are nonlocal. Consequently, functional forms prove to be crucial tomodel results, andwhat economists term‘‘secondbest effects’’ play a role in these outcomes.
Accurate and current data. Given the close link between modeling and policymaking, both the accuracy and the currency of data are important. Unfortunately, there can be a trade-off between accuracy and currency; the most recent data may be only estimates or not entirely survey based. Consequently, professional judgment is needed, and there needs to be a willingness to revise published results as new and better information becomes available.
Model structure determined by the data. The functional forms used to construct applied models must be chosen to allow for important regularities observed in the data. For example, the classical structures of theoretical trade models assume that imports and domestic competing goods are perfect substitutes and that there are no barriers to trade. In this case, the model describes interindustry trade only, cannot support a number of goods that exceed the number of factors of production, and cannot explain bilateral patterns of international trade. To avoid this in applied work, steps are taken to specify alternative model structures that allow for bilateral patterns of intraindustry trade and numbers of goods in excess of numbers of factors of production.
As an illustration of the complexities of applied policy modeling in general and the role of AGE models in particular, consider the case of multilateral Doha Round trade negotiations as described by Francois, van Meijl, and van Tongeren (2005):
Judging the economic impact of aWTO agreement ismassively complex, evenwhen it comes to issues as straightforward as tariff cutting. The eventual Doha Round agreement should lower thousands of individual tariffs in each WTO member country and there are about 150 members. The result would be important shifts of resources among sectors in most nations in the world, along with attendant changes in the prices of goods and productive factors. Due to international trade, the supply and demand factors in each nation affect resource allocations in all other nations. How can economists evaluate the impact of these choices? The most practical way of proceeding is to employ a large-scale computable general equilibrium model that allows simultaneous consideration of all the effects. (352)
This speaks to the utility of applied general equilibrium models and explains why the methodology has evolved from an obscure exercise in applied econometrics to being a key tool for applied policy analysis. Indeed, many national governments use single-country models to assess policy changes, and both national governments and multilateral financial institutions use global models (e.g., the GTAP model described in Hertel 1997 or variants of the linkage model described in van der Mensbrugghe 2006) to assess a large variety of international policy issues.
Overview of Model Structure
In AGE models, it is generally the case that an equation systemis solved for prices that equate supply and demand in all markets simultaneously and satisfy the accounting identities governing economic behavior. Exceptions to this approach exist that allow for disequilibria in some markets (e.g., labor markets). Once the equation system has been specified, the equilibrium is calibrated to a base-year data set (often in the formof a social accounting matrix, or SAM), and the model reproduces the base-year economy in the absence of any policy changes. The calibration ensures that subsequent policy simulations move from an initial position that describes the economy (be it national, regional, or global) and its accounting identities as accurately as possible.
After calibration, the AGE model is used to simulate the effects of alternative policy changes on the economy with reference to the base year (static) or a baseline scenario (dynamic). The model fully captures the flow of income from firms to labor, capital, and other inputs, from each of these inputs to households, and from households back to final demand of various types (household, government, investment, and rest of world or exports). Hence, it remains internally consistent even after introducing policy changes of various kinds.
The policy parameters of an AGE model include tariff rates, quotas, various domestic taxes and subsidies, and a number of behavioral elasticities. The behavioral elasticities play a central role in model results, and this represents an area of inquiry inwhich there is not always complete agreement with regard to appropriate values. Consequently, this is one aspect of applied general equilibrium modeling that needs to be well documented and handledwith care, including the analysis of the sensitivity of model outcomes to assumed elasticity values. Critical in this regard is what is known as the Armington (1969) elasticity, the elasticity of substitution between imports and domestic competing goods.
With a calibrated model in hand, an analyst can simulate the effects of proposed policy changes by comparing the base-year or baseline model solution with a counterfactual solution in which one ormore of the policy parameters have been changed. A comparison of the base-year/baseline and counterfactual equilibria can reveal (depending on model specification) the effects of the policy changes on imports, exports, domestic production, employment, wages, aggregate economic welfare, disaggregated household welfare, and poverty and human development outcomes.
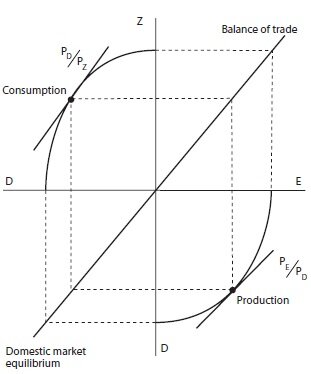
A graphical representation of a simple applied general equi librium model
Standard Framework
A standard framework of applied general equilibrium modes is that described by deMelo and Robinson (1989) and related to the previous contribution of Hazari, Sgro, and Suh (1980) on nontraded goods. In this framework, there are three varieties of goods: an export good (E), an import good (Z), and a nontraded, domestic good (D). Corresponding to these three goods, there are three different prices, PE, PZ, and PD, and three different quantities, E, Z, and D. The graphical representation of this framework is provided in the four quadrants of figure 1. In the southeast quadrant, the country produces two goods, E and D. The concave curve in this quadrant is the country’s production possibilities frontier (PPF) and indicates that there are no economies of scale sufficient to outweigh the increasing opportunity costs of production. In practice, this part of AGE models is actually implemented in two stages, with a constant elasticity of substitution PPF and a constant elasticity of transformation allocation between exports and domestic supply, the latter following Powell and Gruen (1968). Under perfect competition, profit maximization, and full employment of resources, the country produces at a point on the PPF that is tangent to the relative price line PE / PD.
In the northeast quadrant of figure 1, we have a balance of trade line, which relates E and Z. This line tells us what level of imports can exist given the level of exports. As drawn, this balance of trade line is a 45- degree line, but changes in the terms of trade PE / PD will rotate the line either up or down. Capital inflows or outflows will shift the line up or down, respectively, without changing its slope.
In the southwest quadrant of figure 1, the vertical axis plots the supply of the domestic good from the PPF, while the horizontal axis plots the demand for the domestic good. The 45-degree line in this quadrant is simply a domestic market equilibrium condition.
Finally, the northwest quadrant of figure 1 addresses the consumption of goods Z and D. The concave curve in this quadrant is a consumption possibilities frontier (CPF). The consumption possibilities are determined by the PPF, the balance of trade constraint, and domestic market equilibrium. The choice of the point on the CPF will reflect utility maximization in the form of tangency with an indifference curve of a representative household based on product differentiation by country of origin and is typically modeled using a constant elasticity of substitution frameworks as in Armington (1969).
In standard trade theory with incomplete specialization and no transportation costs, bilateral trade patterns remain indeterminate. However, in the framework of figure 1, intraindustry trade is fully captured. In multicountry versions of the model, actual patterns of bilateral, intraindustry tradewill be effectively described in both base and counterfactual equilibria. Finally, nontradability in the framework of figure 1 depends on the price line PE /PD. The higher is this ratio, the more of domestic output will enter into trade. Therefore, nontradability in the applied general equilibrium framework is not fixed by sector but depends on relative prices. Further, unlike Salter (1959), the two traded goods, E and Z, are not aggregated into a single good, and this is more satisfactory for empirical implementation.
Dynamics
The policy changes considered in AGE models have the potential to change both overall income levelsandthe returns tofactors ofproduction. As noted by Francois, McDonald, and Nordtro¨m, ‘‘To the extent that investment hinges on income levels and expected returns, the medium- and longterm results of changes in trading conditions will include induced shifts in the capital stock’’ (1997, 365). Incorporating these considerations into AGE models shifts the analysis fromstatic to dynamic considerations. Dynamic specifications of applied general equilibrium models can vary in a number of respects, but the research on these specifications is now fairly well developed.
When allowed for, dynamic effects show up in model results through a number of paths, including the following: increases in incomes due to trade liberalization and other policy changes raising savings rates, declines in the prices of capital goods increasing real investment, and increasing trade openness (typically measured by sectoral export-to-output ratios) causing sectoral productivity increases. The first and second of these dynamic gains are often referred to as ‘‘medium-run growth effects’’ as identified by Baldwin (1992) and do not depend on any dynamic externalities as emphasized in New Growth Theory. Therefore, they are best viewed as reflecting ‘‘classical’’ or ‘‘old’’ growth theory. In this respect, the first and second paths for dynamic gains are quite firmly reflective of received economic theory.
The third type of dynamic effect is often referred to as the ‘‘procompetitive effects of exporting’’ and can reflect economies of scale in production and trade, learning by doing, standards achievement, and network effects. These potentialities are less standard than themedium-run growth effects, and it is not clear whether they are as automatic as suggested by some model specifications. In addition, there is little empirical evidence with regard to the behavioral elasticities used tomodel these effects. For these reasons, it is prudent to separate out simulations based on these procompetitive effects as indicative of potential rather than as actual, realized gains.
Other Extensions
The standard AGE model considered here has been extended in a number of relevantdirections.These include environmental and natural resource issues (including climate change), industry structure (including imperfect competition), migration, capital flows (including foreign direct investment), financial crises, commodity prices, foreign aid, natural disasters, poverty, and human development. Given this broad coverage of issues that are paramount in assessing the world economy, as well as the more standard applications to trade policies, it is clear that applied general equilibrium models will continue to be an importantmethodology to help us understand the role of national and multilateral policies in the world economy. See also capital accumulation in open economies; gravity models; intraindustry trade; nontraded goods; partial equilibrium models; Swan diagram; terms of trade